In this blog I am going to deal with one of the most popular error detection and correction system which is “Hamming Code”. As known the errors in the electronic systems especially in the digital systems the errors are often occured. Therefore they have to be corrected automatically by the system once they have captured. The errors occurred in the digital systems are due to several phenomenes such us bit change during data transmission, energetic particle (see SEU “Single Event Upset”), magnetic effects, etc. It is mainly used to transmit a data in a noisy channel; it makes it possible to reconstruct the transmitted message even if errors (a limited number), due to noise, have altered the data.
In order to avoid all kind of errors which could cause a data lost we have to implement an error detection and correction bloc in front of the transmission/reception systems. There are several type of error detection systems such us Singleton Bound, Repetition Code, Parity Code, Cyclic Code, Reed-Muller Code, etc. These error detection and correction systems are used according to their complexity, accuracy and computation speed by designers. So today I am going to deal with Hamming Code because it is used by most of systems and become indispensable by designers for the criticial digital electronic systems.
Hamming code principle is following : We fix an k integer and we code each block of m=(2^k)-k-1 bits of data by a block of n=(2^k)-1 bits adding therefore k bits of correction, to some positions at block of m bits. In order to simplify the explanation, each word of length m is encoded by a word of length n with n>= m. The encoding is therefore an application of {0,1)^m toward {0,1}^n . Among the n bits of word-code that we are going to describe, m reproduce the word-source, the n-m are the correction bits (fix-bits) : the transmission rate is the n/m. We show that if two separate words of different code at least in d bits, then the code allows to correct exactly (d-1)/2 errors.
The Hamming Code, for which n=2^k -1 and m=n-k allow us to correct an error; for fixed k and n large. the transmission rate is close to 1. Their description uses the linear algebra modulo 2 or polynomials modulo 2. A word of p bits is represented by a binary vector of p length, that is to say an element of vector space (Z/2.Z)^n, for example for 110 :
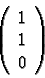
The parity matrix of Hamming Code is a binary matrix of k rows and n columns : The columns contain the binary representation of integers between 1 and n, for exemple:
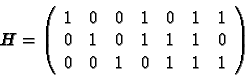
The parity matrix H allows to define the words of the code: These are the vectors c and dimension n such that Hc=0. As this equation defines a vector subspace of (Z/2.Z)^n, it is said to be a liear code, this subspace is of dimension n.
So, as I always say : an example is better than a long speech! Let me show an example of application. We suppose that we receive c` which differs from a word of code c of one bit: c` = c+e where e is the error vector, for example 0100000. As Hc=0, we have Hc’ He because e contains only one bit (for example e=0100000), the Hc’ calculation gives one of the columns of H. If we obtain Hc’= 010, which is the second column of H, it’s because the error is on the second bit, that’s to say e=0100000. So the correction is easy. It remains to be said how the coding and the decoding are carried out, in other words which are the information bits and the correction bits in a word of the code.
The determination of a base of the subspace of equation Hc=0 allows to formulate the coding: if G is the m x n matrix whose rows are the vectors of such a base, Hc=0 is equivalent to c=a.G for a , a line-vector of length m. Thus ‘a’ is encoded by c=a.G; we say that G is the generator matrix of the code.
In the previous example we find easily for example:
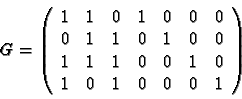
so that the first three bits are those of corrections and next four following being the information bits.
In this blog I tried to explain mathematically how Hamming Code functions. It is used in almost every transmission/receiving system in electronic hardware especially in FPGA chips. At LRN Technology we often use Hamming Code in our systems using VHDL because it is much more used in industry, even in aeronautics. It is a reliable, robust and safe system. There are still other similar systems like those mentioned above but we use it in our systems often and we are far from getting rid of Hamming Code for the moment.